导语:Szilassi多面体就是七面体的一种,有着一个180度的对称轴,属于拓扑结构中的环,被归为凸多面体之中,大约有7个六边形组成,其中的六个面都是凸六边形,每个相邻的面都有共用边,下面就跟着探秘志小编一起来看看吧!
Szilassi多面体是什么?
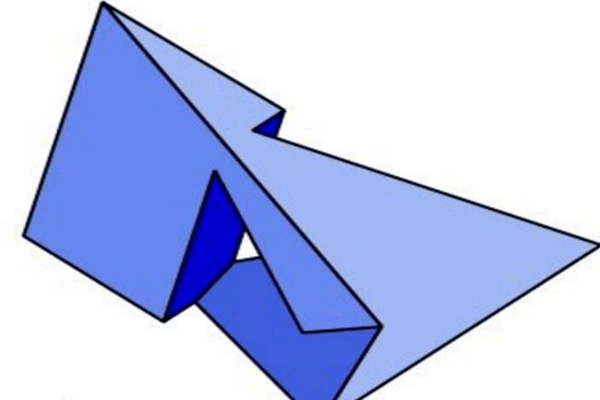
其实Szilassi多面体就是七面体的一种,属于拓扑结构中的环,被归为凸多面体之中,大约有7个六边形组成,其中的六个面都是凸六边形,每个相邻的面都有共用边,虽然Szilassi多面体长的很奇怪,但其实它是个对称立方体,并且有着一个180度的对称轴。
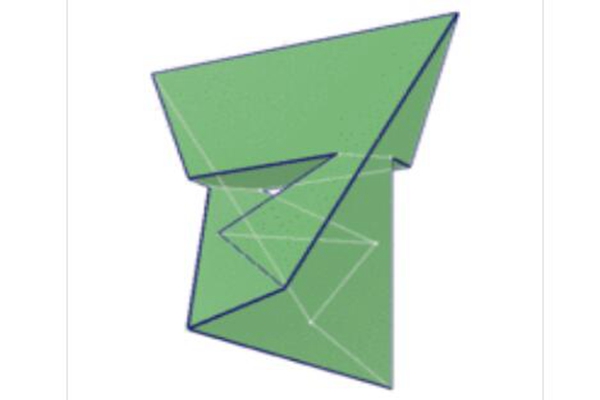
Szilassi多面体之中有三组面全等,且可以运用七种颜色涂满每个相邻的面,也就成了七色定理的最低限,七色定理就是说在亏格为一的环面上染色,必须要7种颜色。Szilassi多面体具有14个顶点和21条边,也是目前已知的每个面都与其他面公用边的多面体之一,还有一个被叫做Heawood graph的四面体,也具有同样的属性。
Szilassi多面体展开图长什么样?

上图就是Szilassi多面体的每个面的投影视图,也就是相当于三视图的感觉,通过这四张图就能大致的感受到Szilassi多面体的样子,比如第二张图就是从侧面看到的样子,而最后一张图就是从顶部看到的样子。

这里是Szilassi多面体的旋转图,能方便看到的更加清晰,对结构更加明了,其实这样看来就像两个三角体互相交叉,并在中间挖出了一块,和正六百胞体不同的是,Szilassi多面体很是比较容易理解的,而且看上去很对称,并不像它的四视图中看到的那么奇怪。
七面体是什么?

其实也就是由七个面组成的多面体,比较常见的有六角锥和五角柱,而Szilassi多面体也是其中一种,不像其他的偶数多面体,由于七是单数,所以根据欧拉公式显示,正七面体是不存在的,因为7不能被整除。
结语:Szilassi多面体虽然不是一个常见的七面体,但也让人们看到了数学的独特,其实数学的趣味性经常表现在几何方面,比如毕达哥拉斯树就是其中一种。




