导语:现在人类比较喜欢进行一些猜想,比如有关未来人类生活的十大猜想等等,在数学界猜想等也是比较盛行的。哥德巴赫也有一大重要猜想,也就是“1 1”猜想,下面和探秘志小编一起了解一下吧。
哥德巴赫猜想
哥德巴赫猜想是最广为人知的数学难题,中学生就都知道这个猜想:“所有大于4的偶数都可以分解成两个素数(质数)的和”。这个猜想有个简称叫做1 1,这是个引起了很多误解的叫法,为什么哥德巴赫猜想会被称作1 1呢?
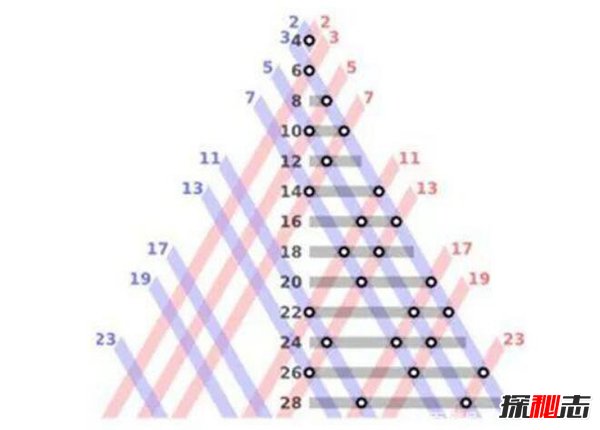
有人说哥德巴赫猜想就是证明1 1=2,这个是基本的一年级数学题,这个说法有点离谱了。还有人说1 1=2不是小学算式,其中1 1代表一个质数加另一个质数,2就代表偶数。首先1不是质数,2也不是哥德巴赫猜想中的偶数,猜想中最小偶数是6。再就是即使1可以代表质数,2也可以代表大于6的偶数,那也不能写成1 1=2,因为这个算式语言表述应该是:“两个质数的和是一个偶数”。这个也比较简单啊,根本不需要哥德巴赫猜。
为什么被称为1 1呢

哥德巴赫猜想常被称为1 1,没有后边的=2。那么被称为1 1的具体原因是什么呢?哥德巴赫猜想虽然看着比较简单,但是实际上看懂题目了不一定会做,甚至很多人连思路都没有,其主要包含四个方面:殆素数,例外集合,小变量的三素数定理以及几乎哥德巴赫问题。
殆素数
殆素数就是素因子个数不多的正整数。现设N是偶数,虽然不能证明N是两个素数之和,但足以证明它能够写成两个殆素数的和,即N=A B,其中A和B的素因子个数都不太多,譬如说素因子个数不超过10。用“a b”来表示如下命题:每个大偶数N都可表为A B,其中A和B的素因子个数分别不超过a和b。显然,哥德巴赫猜想就可以写成"1 1"。在这一方向上的进展都是用所谓的筛法得到的。

“a b”问题的推进
1920年,挪威的布朗证明了“9 9”。
1924年,德国的拉特马赫证明了“7 7”。
1932年,英国的埃斯特曼证明了“6 6”。
1937年,意大利的蕾西先后证明了“5 7”, “4 9”, “3 15”和“2 366”。
1938年,苏联的布赫夕太勃证明了“5 5”。
1940年,苏联的布赫夕太勃证明了“4 4”。
1956年,中国的王元证明了“3 4”。稍后证明了 “3 3”和“2 3”。
1948年,匈牙利的瑞尼证明了“1 c”,其中c是一很大的自然数。
1962年,中国的潘承洞和苏联的巴尔巴恩证明了“1 5”, 中国的王元证明了“1 4”。
1965年,苏联的布赫 夕太勃和小维诺格拉多夫,及意大利的朋比利证明了“1 3 ”。
1966年,中国的陈景润证明了 “1 2 ”。

到这里研究就截止了,几十年过去了,仍然没有其他进展,甚至有很多数学家认为陈景润的定理是殆素数方法的极限,也就是说殆素数的思路根本证明不了哥德巴赫猜想。
虽然这种办法还可以最终证明哥德巴赫猜想,但却给了哥德巴赫猜想一个令人误解的名字——1 1。
结语:这个研究过程是不是非常有趣,当然数学的发展也不是一帆风顺的,在过程中也有数学三次重大危机,但是最终结果是好的就够了。




