所谓的芝诺悖论在正常人眼里是完全不可能实现的,因为这个悖论涉及了时间与空间的问题。比如你永远都追不上一只乌龟,一支被射出去的箭实际上是静止的,这听上去十分的不可思议,但是看完下面的故事与解释之后,你应该会明白这个悖论的精妙所在。
芝诺悖论:阿基里斯追不上乌龟、从A点到B点永不能到达、飞矢不动、游行队伍
世界十大悖论:费米悖论、乌鸦悖论、黄油猫悖论、芝诺悖论、霍金悖论、理发师悖论、外祖母悖论、上帝悖论、说谎者悖论、伊壁鸠鲁悖论
一、阿基里斯追不上乌龟
这是芝诺悖论中最著名的一个悖论,一个善跑健将永远都追不上一只近在咫尺的乌龟。阿基里斯是古希腊神话中善跑的英雄。在他和乌龟的竞赛中,他速度为乌龟十倍,乌龟在前面100米跑,他在后面追,但他不可能追上乌龟。当阿基里斯追到100米,乌龟的出发点时,乌龟已经又向前爬了10米,于是,一个新的起点产生了。
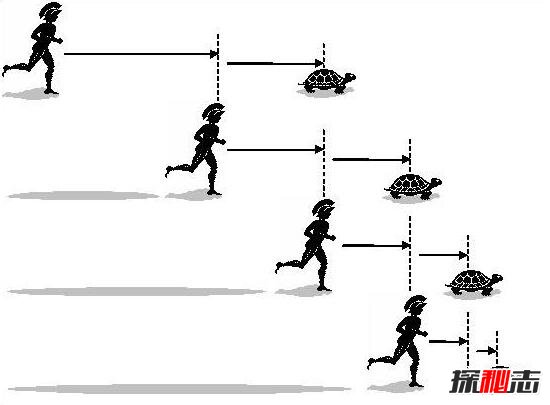
阿基里斯必须继续追,而当他追到乌龟爬的这10米时,乌龟又已经向前爬了1米,阿基里斯只能再追向那个1米。就这样,乌龟会制造出无穷个起点,它总能在起点与自己之间制造出一个距离,不管这个距离有多小,但只要乌龟不停地奋力向前爬,阿基里斯就永远也追不上乌龟!

悖论解释:因为乌龟爬到B点,而你不是同时到达B点的话,那你到达的B点就不是乌龟到达的B点,因为时间的不同,你的B点永远也不是乌龟的B点。这虽然在空间上是同一地点,但是在时间上是永远不相同的,所以你永远追不上。
二、从A点到B点永不能到达

一个人从A点走到B点,必先走完路程的1/2,然后走完剩下的1/2时,必须走完剩下总路程的1/2,以此类推,再走完剩下的1/2,又可以分出一个1/2……”如此循环下去,由于1/2总可以不停的分解下去,则一个人永远不能到终点B。当A,B无限接近的时候,也就是说人无法运动,只能静止!

悖论解释:假设此人速度不变,走一段的时间每次除以2,时间为实际需要时间的1/2 1/4 1/8 ......,则时间限制在实际需要时间以内,即此人与目的地距离可以为任意小,却到不了。实际上是这个芝诺悖论本身限定了时间,当然到达不了。




